I’ll start this post by tying up some loose ends from last time. Before we get going there’s no better recommendation for uplifting listening than this marvellous recording. Hopefully it’ll help motivate and inspire you (and I) as we journey deeper into the weird and wonderful world of algebra and geometry.
I promised a proof that for algebraically closed fields 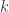 every Zariski open set is dense in the Zariski topology. Quite a mouthful at this stage of a post, I admit. Basically what I’m showing is that Zariski open sets are really damn big, only in a mathematically precise way. But what of this ‘algebraically closed’ nonsense? Time for a definition.
every Zariski open set is dense in the Zariski topology. Quite a mouthful at this stage of a post, I admit. Basically what I’m showing is that Zariski open sets are really damn big, only in a mathematically precise way. But what of this ‘algebraically closed’ nonsense? Time for a definition.
Definition 3.1 A field 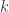 is algebraically closed if every nonconstant polynomial in
is algebraically closed if every nonconstant polynomial in ![k[x]](https://s0.wp.com/latex.php?latex=k%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) has a root in
has a root in 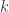 .
.
Let’s look at a few examples. Certainly 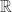 isn’t algebraically closed. Indeed the polynomial
isn’t algebraically closed. Indeed the polynomial 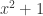 has no root in
has no root in 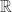 . By contrast
. By contrast 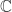 is algebraically closed, by virtue of the Fundamental Theorem of Algebra. Clearly no finite field is algebraically closed. Indeed suppose
is algebraically closed, by virtue of the Fundamental Theorem of Algebra. Clearly no finite field is algebraically closed. Indeed suppose  then
then  has no root in
has no root in 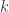 . We’ll take a short detour to exhibit another large class of algebraically closed fields.
. We’ll take a short detour to exhibit another large class of algebraically closed fields.
Definition 3.2 Let  be fields with
be fields with  . We say that
. We say that  is a field extension of
is a field extension of 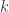 and write
and write  for this situation. If every element of
for this situation. If every element of  is the root of a polynomial in
is the root of a polynomial in ![k[x]](https://s0.wp.com/latex.php?latex=k%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) we call
we call  an algebraic extension. Finally we say that the algebraic closure of
an algebraic extension. Finally we say that the algebraic closure of 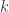 is the algebraic extension
is the algebraic extension  of
of 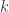 which is itself algebraically closed.
which is itself algebraically closed.
(For those with a more technical background, recall that the algebraic closure is unique up to 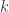 -isomorphisms, provided one is willing to apply Zorn’s Lemma).
-isomorphisms, provided one is willing to apply Zorn’s Lemma).
The idea of algebraic closure gives us a pleasant way to construct algebraically closed fields. However it gives us little intuition about what these fields ‘look like’. An illustrative example is provided by the algebraic closure of the finite field of order 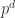 for
for 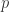 prime. We’ll write
prime. We’ll write  for this field, as is common practice. It’s not too hard to prove the following
for this field, as is common practice. It’s not too hard to prove the following
Theorem 3.3 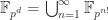
Proof Read this PlanetMath article for details.
Now we’ve got a little bit of an idea what algebraically closed fields might look like! In particular we’ve constructed such fields with characteristic 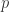 for all
for all 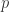 . From now on we shall boldly assume that for our purposes
. From now on we shall boldly assume that for our purposes
every field 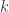 is algebraically closed
is algebraically closed
I imagine that you may have an immediate objection. After all, I’ve been recommending that you use  to gain an intuition about
to gain an intuition about  . But we’ve just seen that
. But we’ve just seen that 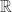 is not algebraically closed. Seems like we have an issue.
is not algebraically closed. Seems like we have an issue.
At this point I have to wave my hands a bit. Since  is a subset of
is a subset of  we can recover many (all?) of the geometrical properties we want to study in
we can recover many (all?) of the geometrical properties we want to study in  by examining them in
by examining them in  and projecting appropriately. Moreover since
and projecting appropriately. Moreover since  can be identified with
can be identified with  in the Euclidean topology, our knowledge of
in the Euclidean topology, our knowledge of  is still a useful intuitive guide.
is still a useful intuitive guide.
However we should be aware that when we are examining affine plane curves with  they are in some sense
they are in some sense  dimensional objects – subsets of
dimensional objects – subsets of  . If you can imagine
. If you can imagine  dimensional space then you are a better person than I! That’s not to say that these basic varieties are completely intractable though. By looking at projections in
dimensional space then you are a better person than I! That’s not to say that these basic varieties are completely intractable though. By looking at projections in 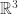 and
and  we can gain a pretty complete geometric insight. And this will soon be complemented by our burgeoning algebraic understanding.
we can gain a pretty complete geometric insight. And this will soon be complemented by our burgeoning algebraic understanding.
Now that I’ve finished rambling, here’s the promised proof!
Lemma 3.4 Every nonempty Zariski open subset of 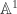 is dense.
is dense.
Proof Recall that ![k[x]](https://s0.wp.com/latex.php?latex=k%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is a principal ideal domain. Thus any ideal
is a principal ideal domain. Thus any ideal ![I\subset k[x]](https://s0.wp.com/latex.php?latex=I%5Csubset+k%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) may be written
may be written 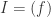 . But
. But 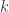 algebraically closed so
algebraically closed so 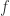 splits into linear factors. In other words
splits into linear factors. In other words  . Hence the nontrivial Zariski closed subsets of
. Hence the nontrivial Zariski closed subsets of 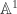 are finite, so certainly the Zariski open subsets of
are finite, so certainly the Zariski open subsets of 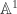 are dense.
are dense. 
I believe that the general case is true for the complement of an irreducible variety, a concept which will be introduced next. However I haven’t been able to find a proof, so have asked here.
How do varieties split apart? This is a perfectly natural question. Indeed many objects, both in mathematics and the everyday world, are made of some fundamental building block. Understanding this ‘irreducible atom’ gives us an insight into the properties of the object itself. We’ll thus need a notion for what constitutes an ‘irreducible’ or ‘atomic’ variety.
Definition 3.5 An affine variety  is called reducible if one can write
is called reducible if one can write  with
with  proper subsets of
proper subsets of  . If
. If  is not reducible, we call it irreducible.
is not reducible, we call it irreducible.
This seems like a good and intuitive way of defining irreducibility. But we don’t yet know that every variety can be constructed from irreducible building blocks. We’ll use the next few minutes to pursue such a theorem.
As an aside, I’d better tell you about some notational confusion that sometimes creeps in. Some authors use the term algebraic set for my term affine variety. Such books will often use the term affine variety to mean irreducible algebraic set. For the time being I’ll stick to my guns, and use the word irreducible when it’s necessary!
Before we go theorem hunting, let’s get an idea about what irreducible varieties look like by examining some examples. The ‘preschool’ example is that  is reducible, for indeed
is reducible, for indeed  . This is neither very interesting nor really very informative, however.
. This is neither very interesting nor really very informative, however.
A better example is the fact that 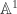 is irreducible. To see this, recall that earlier we found that the only proper subvarieties of
is irreducible. To see this, recall that earlier we found that the only proper subvarieties of 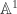 are finite. But
are finite. But 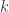 is algebraically closed, so infinite. Hence we cannot write
is algebraically closed, so infinite. Hence we cannot write 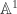 as the union of two proper subvarities!
as the union of two proper subvarities!
What about the obvious generalization of this to  ? Turns out that it is indeed true, as we might expect. For the sake of formality I’ll write it up as a lemma.
? Turns out that it is indeed true, as we might expect. For the sake of formality I’ll write it up as a lemma.
Lemma 3.6  is irreducible
is irreducible
Proof Suppose we could write  . By Lemma 2.5 we know that
. By Lemma 2.5 we know that 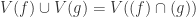 . But
. But  so
so  again by Lemma 2.5. Conversely if
again by Lemma 2.5. Conversely if  then either
then either 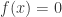 or
or  , so
, so 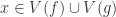 . This shows that
. This shows that  .
.
Now  immediately tells us
immediately tells us 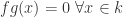 . Suppose that
. Suppose that 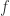 is nonzero. We’ll prove that
is nonzero. We’ll prove that 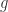 is the zero polynomial by induction on
is the zero polynomial by induction on  . Then
. Then  so
so  not irreducible, as required.
not irreducible, as required.
We first note that since 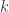 algebraically closed
algebraically closed 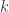 infinite. For
infinite. For  suppose
suppose  . Then
. Then  are each zero at finite sets of points. Thus since
are each zero at finite sets of points. Thus since 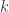 infinite,
infinite,  is not the zero polynomial, a contradiction.
is not the zero polynomial, a contradiction.
Now let 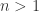 . Consider
. Consider  nonzero polynomials in
nonzero polynomials in ![k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Fix
. Fix 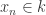 . Then
. Then  polynomials in
polynomials in ![k[\mathbb{A}^{n-1}]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5E%7Bn-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . For some
. For some 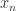 ,
,  nonzero as polynomials in
nonzero as polynomials in ![k[\mathbb{A}^{n-1}]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5E%7Bn-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . By the induction hypothesis
. By the induction hypothesis  . This completes the induction.
. This completes the induction. 
I’ll quickly demonstrate that  is quite strange, when considered as a topological space with the Zariski topology! Indeed let
is quite strange, when considered as a topological space with the Zariski topology! Indeed let 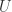 and
and 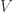 be two nonempty open subsets. Then
be two nonempty open subsets. Then  . Otherwise
. Otherwise  would be proper closed subsets (affine subvarieties) which covered
would be proper closed subsets (affine subvarieties) which covered  , violating irreducibility. This is very much not what happens in the Euclidean topology! Similarly we now have a rigorous proof that an open subset
, violating irreducibility. This is very much not what happens in the Euclidean topology! Similarly we now have a rigorous proof that an open subset 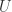 of
of  is dense. Otherwise
is dense. Otherwise  and
and  would be proper subvarieties covering
would be proper subvarieties covering  .
.
It’s all very well looking for direct examples of irreducible varieties, but in doing so we’ve forgotten about algebra! In fact algebra gives us a big helping hand, as the following theorem shows. For completeness we first recall the definition of a prime ideal.
Definition 3.7 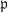 is a prime ideal in
is a prime ideal in 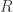 iff whenever
iff whenever  we have
we have 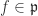 or
or  . Equivalently
. Equivalently 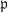 is prime iff
is prime iff  is an integral domain.
is an integral domain.
Theorem 3.8 Let  be a nonempty affine variety. Then
be a nonempty affine variety. Then  irreducible iff
irreducible iff  a prime ideal.
a prime ideal.
Proof [“ “] Suppose
“] Suppose  not prime. Then
not prime. Then ![\exists f,g \in k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=%5Cexists+f%2Cg+%5Cin+k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) with
with 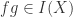 but
but  . Let
. Let  and
and  . Further define
. Further define  . Then
. Then 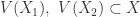 so proper subsets of
so proper subsets of  . On the other hand
. On the other hand 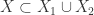 . Indeed if
. Indeed if  then
then  so
so 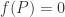 or
or  so
so 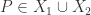 .
.
[“ “] Suppose
“] Suppose  is reducible, that is
is reducible, that is  proper subvarieties of
proper subvarieties of  with
with 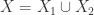 . Since
. Since 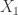 a proper subvariety of
a proper subvariety of  there must exist some element
there must exist some element 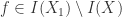 . Similarly we find
. Similarly we find 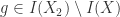 . Hence
. Hence 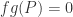 for all
for all 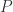 in
in  , so certainly
, so certainly 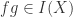 . But this means that
. But this means that  is not prime.
is not prime. 
This easy theorem is our first real taste of the power that abstract algebra lends to the study of geometry. Let’s see it in action.
Recall that a nonzero principal ideal of the ring ![k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is prime iff it is generated by an irreducible polynomial. This is an easy consequence of the fact that
is prime iff it is generated by an irreducible polynomial. This is an easy consequence of the fact that ![k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is a UFD. Indeed a nonzero principal ideal is prime iff it is generated by a prime element. But in a UFD every prime is irreducible, and every irreducible is prime!
is a UFD. Indeed a nonzero principal ideal is prime iff it is generated by a prime element. But in a UFD every prime is irreducible, and every irreducible is prime!
Using the theorem we can say that every irreducible polynomial 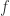 gives rise to an irreducible affine hypersurface
gives rise to an irreducible affine hypersurface  s.t.
s.t. 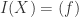 . Note that we cannot get a converse to this – there’s nothing to say that
. Note that we cannot get a converse to this – there’s nothing to say that  must be principal in general.
must be principal in general.
Does this generalise to ideals generated by several irreducible polynomials? We quickly see the answer is no. Indeed take  in
in ![k[\mathbb{A}^2]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5E2%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . These are both clearly irreducible, but
. These are both clearly irreducible, but  is not prime. We can see this in two ways. Algebraically
is not prime. We can see this in two ways. Algebraically  but
but  . Geometrically, recall Lemma 2.5 (3). Also note that by definition
. Geometrically, recall Lemma 2.5 (3). Also note that by definition  . Hence
. Hence  . But
. But 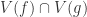 is clearly just two distinct points (the intersection of the line with the circle). Hence it is reducible, and by our theorem
is clearly just two distinct points (the intersection of the line with the circle). Hence it is reducible, and by our theorem  cannot be prime.
cannot be prime.
We can also use the theorem to exhibit a more informative example of a reducible variety. Consider  . Clearly
. Clearly  is not prime for
is not prime for  but
but  . Noting that
. Noting that  we see that geometrically
we see that geometrically  is the union of the
is the union of the  -axis and the parabola
-axis and the parabola  , by Lemma 2.5.
, by Lemma 2.5.
Having had such success with prime ideals and irreducible varieties, we might think – what about maximal ideals? Turns out that they have a role to play too. Note that maximal ideals are automatically prime, so any varieties they generate will certainly be irreducible.
Definition 3.9 An ideal  of
of 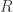 is said to be maximal if whenever
is said to be maximal if whenever 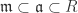 either
either  or
or 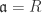 . Equivalently
. Equivalently  is maximal iff
is maximal iff  is a field.
is a field.
Theorem 3.10 An affine variety  in
in  is a point iff
is a point iff  is a maximal ideal.
is a maximal ideal.
Proof [“ “] Let
“] Let 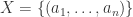 be a single point. Then clearly
be a single point. Then clearly  . But
. But ![k[\mathbb{A}^n]/I(X)](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D%2FI%28X%29&bg=ffffff&fg=2b2b2b&s=0&c=20201002) a field. Indeed
a field. Indeed ![k[\mathbb{A}^n]/I(X)](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D%2FI%28X%29&bg=ffffff&fg=2b2b2b&s=0&c=20201002) isomorphic to
isomorphic to 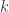 itself, via the isomorphism
itself, via the isomorphism  . Hence
. Hence  maximal.
maximal.
[“ “] We’ll see this next time. In fact all we need to show is that
“] We’ll see this next time. In fact all we need to show is that  are the only maximal ideals.
are the only maximal ideals. 
Theorems 3.8 and 3.10 are a promising start to our search for a dictionary between algebra and geometry. But they are unsatisfying in two ways. Firstly they tell us nothing about the behaviour of reducible affine varieties – a very large class! Secondly it is not obvious how to use 3.8 to construct irreducibly varieties in general. Indeed there is an inherent asymmetry in our knowledge at present, as I shall now demonstrate.
Given an irreducible variety  we can construct it’s ideal
we can construct it’s ideal  and be sure it is prime, by Theorem 3.8. Moreover we know by Lemma 2.5 that
and be sure it is prime, by Theorem 3.8. Moreover we know by Lemma 2.5 that 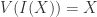 , a pleasing correspondence. However, given a prime ideal
, a pleasing correspondence. However, given a prime ideal  we cannot immediately say that
we cannot immediately say that 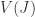 is prime. For in Lemma 2.5 there was nothing to say that
is prime. For in Lemma 2.5 there was nothing to say that  , so Theorem 3.8 is useless. We clearly need to find a set of ideals for which
, so Theorem 3.8 is useless. We clearly need to find a set of ideals for which  holds, and hope that prime ideals are a subset of this.
holds, and hope that prime ideals are a subset of this.
It turns out that such a condition is satisfied by a class called radical ideals. Next time we shall prove this, and demonstrate that radical ideals correspond exactly to algebraic varieties. This will provide us with the basic dictionary of algebraic geometry, allowing us to proceed to deeper results. The remainder of this post shall be devoted to radical ideals, and the promised proof of an irreducible decomposition.
Definition 3.11 Let  be an ideal in a ring
be an ideal in a ring 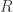 . We define the radical of
. We define the radical of  to be the ideal
to be the ideal  . We say that
. We say that  is a radical ideal if
is a radical ideal if  .
.
(That  is a genuine ideal needs proof, but this is merely a trivial check of the axioms).
is a genuine ideal needs proof, but this is merely a trivial check of the axioms).
At first glance this appears to be a somewhat arbitrary definition, though the nomenclature should seem sensible enough. To get a more rounded perspective let’s introduce some other concepts that will become important later.
Definition 3.12 A polynomial function or regular function on an affine variety  is a map
is a map  which is defined by the restriction of a polynomial in
which is defined by the restriction of a polynomial in ![k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) to
to  . More explicitly it is a map
. More explicitly it is a map 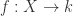 with
with 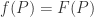 for all
for all  where
where ![F\in k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=F%5Cin+k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) some polynomial.
some polynomial.
These are eminently reasonable quantities to be interested in. In many ways they are the most obvious functions to define on affine varieties. Regular functions are the analogues of smooth functions in differential geometry, or continuous functions in topology. They are the canonical maps.
It is obvious that a regular function 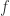 cannot in general uniquely define the polynomial
cannot in general uniquely define the polynomial 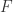 giving rise to it. In fact suppose
giving rise to it. In fact suppose  . Then
. Then  on
on  so
so 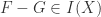 . This simple observation explains the implicit claim in the following definition.
. This simple observation explains the implicit claim in the following definition.
Definition 3.13 Let  be an affine variety. The coordinate ring
be an affine variety. The coordinate ring ![k[X]](https://s0.wp.com/latex.php?latex=k%5BX%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is the ring
is the ring ![k[\mathbb{A}^n]|_X=k[\mathbb{A}^n]/I(X)](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D%7C_X%3Dk%5B%5Cmathbb%7BA%7D%5En%5D%2FI%28X%29&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . In other words the coordinate ring is the ring of all regular functions on
. In other words the coordinate ring is the ring of all regular functions on  .
.
This definition should also appear logical. Indeed we define the space of continuous functions in topology and the space of smooth functions in differential geometry. The coordinate ring is merely the same notion in algebraic geometry. The name ‘coordinate ring’ arises since clearly ![k[X]](https://s0.wp.com/latex.php?latex=k%5BX%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is generated by the coordinate functions
is generated by the coordinate functions  restricted to
restricted to  . The reason for our notation
. The reason for our notation ![k[x_1,\dots ,x_n]=k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=k%5Bx_1%2C%5Cdots+%2Cx_n%5D%3Dk%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) should now be obvious. Note that the coordinate ring is trivially a finitely generated
should now be obvious. Note that the coordinate ring is trivially a finitely generated 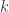 -algebra.
-algebra.
The coordinate ring might seem a little useless at present. We’ll see in a later post that it has a vital role in allowing us to apply our dictionary of algebra and geometry to subvarieties. To avoid confusion we’ll stick to ![k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) for the near future. The reason for introducing coordinate rings was to link them to radical ideals. We’ll do this via two final definitions.
for the near future. The reason for introducing coordinate rings was to link them to radical ideals. We’ll do this via two final definitions.
Definition 3.14 An element  of a ring
of a ring 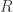 is called nilpotent if
is called nilpotent if  some positive integer
some positive integer  s.t.
s.t. 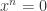 .
.
Definition 3.15 A ring 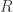 is reduced if
is reduced if  is its only nilpotent element.
is its only nilpotent element.
Lemma 3.16  is reduced iff
is reduced iff 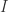 is radical.
is radical.
Proof Let  be a nilpotent element of
be a nilpotent element of  i.e.
i.e.  . Hence
. Hence  so by definition
so by definition 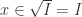 . Conversely let
. Conversely let  . Then
. Then  in
in  so
so  i.e.
i.e. 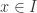 . $/blacksquare$
. $/blacksquare$
Putting this all together we immediately see that the coordinate ring ![k[X]](https://s0.wp.com/latex.php?latex=k%5BX%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is a reduced, finitely generated
is a reduced, finitely generated 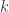 -algebra. That is, provided we assume that for an affine variety
-algebra. That is, provided we assume that for an affine variety  ,
,  is radical, which we’ll prove next time. It’s useful to quickly see that these properties characterise coordinate rings of varieties. In fact given any reduced, finitely generated
is radical, which we’ll prove next time. It’s useful to quickly see that these properties characterise coordinate rings of varieties. In fact given any reduced, finitely generated 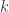 -algebra
-algebra 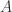 we can construct a variety
we can construct a variety  with
with ![k[X]=A](https://s0.wp.com/latex.php?latex=k%5BX%5D%3DA&bg=ffffff&fg=2b2b2b&s=0&c=20201002) as follows.
as follows.
Write ![A=k[a_1,\dots ,a_n]](https://s0.wp.com/latex.php?latex=A%3Dk%5Ba_1%2C%5Cdots+%2Ca_n%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) and define a surjective homomorphism
and define a surjective homomorphism ![\pi:k[\mathbb{A}^n]\rightarrow A, \ x_i\mapsto a_i](https://s0.wp.com/latex.php?latex=%5Cpi%3Ak%5B%5Cmathbb%7BA%7D%5En%5D%5Crightarrow+A%2C+%5C+x_i%5Cmapsto+a_i&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Let
. Let 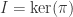 and
and 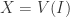 . By the isomorphism theorem
. By the isomorphism theorem ![A = k[\mathbb{A}^n]/I](https://s0.wp.com/latex.php?latex=A+%3D+k%5B%5Cmathbb%7BA%7D%5En%5D%2FI&bg=ffffff&fg=2b2b2b&s=0&c=20201002) so
so 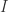 is radical since
is radical since 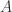 reduced. But then by our theorem next time
reduced. But then by our theorem next time  an affine variety, with coordinate ring
an affine variety, with coordinate ring 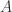 .
.
We’ve come a long way in this post, and congratulations if you’ve stayed with me through all of it! Let’s survey the landscape. In the background we have abstract algebra – systems of equations whose solutions we want to study. In the foreground are our geometrical ideas – affine varieties which represent solutions to the equations. These varieties are built out of irreducible blocks, like Lego. We can match up ideals and varieties according to various criteria. We can also study maps from geometrical varieties down to the ground field using the coordinate ring.
Before I go here’s the promised proof that irreducible varieties really are the building blocks we’ve been talking about.
Theorem 3.17 Every affine variety  has a unique decomposition as
has a unique decomposition as  up to ordering, where the
up to ordering, where the  are irreducible components and
are irreducible components and  for
for 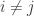 .
.
Proof (Existence) An affine variety  is either irreducible or
is either irreducible or  with
with 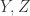 proper subset of
proper subset of  . We similarly may decompose
. We similarly may decompose 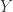 and
and 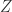 if they are reducible, and so on. We claim that this process stops after finitely many steps. Suppose otherwise, then
if they are reducible, and so on. We claim that this process stops after finitely many steps. Suppose otherwise, then  contains an infinite sequence of subvarieties
contains an infinite sequence of subvarieties  . By Lemma 2.5 (5) & (7) we have
. By Lemma 2.5 (5) & (7) we have  . But
. But ![k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) a Noetherian ring by Hilbert’s Basis Theorem, and this contradicts the ascending chain condition! To satisfy the
a Noetherian ring by Hilbert’s Basis Theorem, and this contradicts the ascending chain condition! To satisfy the 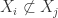 condition we simply remove any such
condition we simply remove any such  that exist in the decomposition we’ve found.
that exist in the decomposition we’ve found.
(Uniqueness) Suppose we have another decomposition  with
with  for
for 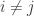 . Then
. Then  . Since
. Since  is irreducible we must have
is irreducible we must have  for some
for some 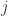 . In particular
. In particular  . But now by doing the same with the
. But now by doing the same with the  and
and 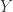 reversed we find
reversed we find  width
width  . But this forces
. But this forces 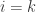 and
and  . But
. But 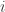 was arbitrary, so we are done.
was arbitrary, so we are done. 
If you’re interested in calculating some specific examples of ideals and their associated varieties have a read about Groebner Bases. This will probably become a topic for a post at some point, loosely based on the ideas in Hassett’s excellent book. This question is also worth a skim.
I leave you with this enlightening MathOverflow discussion , tackling the irreducibility of polynomials in two variables. Although some of the material is a tad dense, it’s nevertheless interesting, and may be a useful future reference!
matrices modulo a
action, which has homogeneous “Plücker” coordinates given by the
minors. Of course, these are not coordinates in the true sense, for they are overcomplete. In particular there exist quadratic Plücker relations between the minors. In principle then, you only need a subset of the homogeneous coordinates to cover the whole Grassmannian.
minor is positive. Of course, you only need to check this for some subset of the Plücker coordinates, but it’s tricky to determine which ones. In the first talk of the day Lauren Williams showed how you can elegantly extract this information from paths on a graph!
-dimensional algebra generated by
with the relation that
for some parameter
different from
. The matrices that linearly transform this plane are then constrained in their entries for consistency. There’s a natural way to build these up into higher dimensional quantum matrices. The quantum Grassmannian is constructed exactly as above, but with these new-fangled quantum matrices!
super-Yang-Mills. Stop press! Maybe it works for non-planar theories as well. In any case, it’s further evidence that Grassmannia are the future.