It’s time to prove the central result of elementary algebraic geometry. Mostly it’s referred to as Hilbert’s Nullstellensatz. This German term translates precisely to the title of this post. Indeed ‘Null’ means ‘zero’, ‘stellen’ means to exist and ‘Satz’ means theorem. But referring to it merely as an existence theorem for zeroes is inadequate. Its real power is in setting up a correspondence between algebra and geometry.
Are you sitting comfortably? Grab a glass of water (or wine if you prefer). Settle back and have a peruse of these theorems. This is your first glance into the heart of a magical subject.
(In many texts these theorems are all referred to as the Nullstellensatz. I think this is both pointless and confusing, so have renamed them! If you have any comments or suggestions about these names please let me know).
Theorem 4.1 (Hilbert’s Nullstellensatz) Let ![J\subsetneq k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=J%5Csubsetneq+k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) be a proper ideal of the polynomial ring. Then
be a proper ideal of the polynomial ring. Then  . In other words, for every nontrivial ideal there exists a point which simulataneously zeroes all of its elements.
. In other words, for every nontrivial ideal there exists a point which simulataneously zeroes all of its elements.
Theorem 4.2 (Maximal Ideal Theorem) Every maximal ideal ![\mathfrak{m}\subset k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=%5Cmathfrak%7Bm%7D%5Csubset+k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is of the form
is of the form 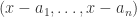 for some
for some  . In other words every maximal ideal is the ideal of some single point in affine space.
. In other words every maximal ideal is the ideal of some single point in affine space.
Theorem 4.3 (Correspondence Theorem) For every ideal ![J\subset k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=J%5Csubset+k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) we have
we have  .
.
We’ll prove all of these shortly. Before that let’s have a look at some particular consequences. First note that 4.1 is manifestly false if 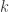 is not algebraically closed. Consider for example
is not algebraically closed. Consider for example  and
and  . Then certainly
. Then certainly 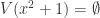 . Right then. From here on in we really must stick just to algebraically closed fields.
. Right then. From here on in we really must stick just to algebraically closed fields.
Despite having the famous name, 4.1 not really immediately useful. In fact we’ll see its main role is as a convenient stopping point in the proof of 4.3 from 4.2. The maximal ideal theorem is much more important. It precisely provides the converse to Theorem 3.10. But it is the correspondence theorem that is of greatest merit. As an immediate corollary of 4.3, 3.8 and 3.10 (recalling that prime and maximal ideals are radical) we have
Corollary 4.4 The maps  as defined in 1.2 and 2.4 give rise to the following bijections
as defined in 1.2 and 2.4 give rise to the following bijections
![\{\textrm{affine varieties in }\mathbb{A}^n\} \leftrightarrow \{\textrm{radical ideals in } k[\mathbb{A}^n]\}](https://s0.wp.com/latex.php?latex=%5C%7B%5Ctextrm%7Baffine+varieties+in+%7D%5Cmathbb%7BA%7D%5En%5C%7D+%5Cleftrightarrow+%5C%7B%5Ctextrm%7Bradical+ideals+in+%7D+k%5B%5Cmathbb%7BA%7D%5En%5D%5C%7D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
![\{\textrm{irreducible varieties in }\mathbb{A}^n\} \leftrightarrow \{\textrm{prime ideals in } k[\mathbb{A}^n]\}](https://s0.wp.com/latex.php?latex=%5C%7B%5Ctextrm%7Birreducible+varieties+in+%7D%5Cmathbb%7BA%7D%5En%5C%7D+%5Cleftrightarrow+%5C%7B%5Ctextrm%7Bprime+ideals+in+%7D+k%5B%5Cmathbb%7BA%7D%5En%5D%5C%7D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
![\{\textrm{points in }\mathbb{A}^n\} \leftrightarrow \{\textrm{maximal ideals in } k[\mathbb{A}^n]\}](https://s0.wp.com/latex.php?latex=%5C%7B%5Ctextrm%7Bpoints+in+%7D%5Cmathbb%7BA%7D%5En%5C%7D+%5Cleftrightarrow+%5C%7B%5Ctextrm%7Bmaximal+ideals+in+%7D+k%5B%5Cmathbb%7BA%7D%5En%5D%5C%7D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
Proof We’ll prove the first bijection explicitly, for it is so rarely done in the literature. The second and third bijections follow from the argument for the first and 3.8, 3.10. Let  be a radical ideal in
be a radical ideal in ![k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Then
. Then 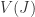 certainly an affine variety so
certainly an affine variety so 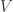 well defined. Moreover
well defined. Moreover 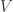 is injective. For suppose
is injective. For suppose  radical with
radical with  . Then
. Then  and thus by 4.3
and thus by 4.3 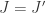 . It remains to prove that
. It remains to prove that 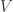 surjective. Take
surjective. Take 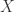 an affine variety. Then
an affine variety. Then  an ideal with
an ideal with  by Lemma 2.5. But
by Lemma 2.5. But 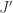 not necessarily radical. Let
not necessarily radical. Let 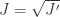 a radical ideal. Then by 4.3
a radical ideal. Then by 4.3  . So
. So 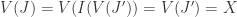 by 2.5. This completes the proof.
by 2.5. This completes the proof. 
We’ll see in the next post that we need not restrict our attention to  . In fact using the coordinate ring we can gain a similar correspondence for the subvarieties of any given variety. This will lead to an advanced introduction to the language of schemes. With these promising results on the horizon, let’s get down to business. We’ll begin by recalling a definition and a theorem.
. In fact using the coordinate ring we can gain a similar correspondence for the subvarieties of any given variety. This will lead to an advanced introduction to the language of schemes. With these promising results on the horizon, let’s get down to business. We’ll begin by recalling a definition and a theorem.
Definition 4.5 A finitely generated 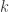 -algebra is a ring
-algebra is a ring 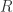 s.t.
s.t. ![R \cong k[a_1,\dots,a_n]](https://s0.wp.com/latex.php?latex=R+%5Ccong+k%5Ba_1%2C%5Cdots%2Ca_n%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) for some
for some  . A finite
. A finite 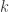 -algebra is a ring
-algebra is a ring 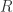 s.t.
s.t.  .
.
Observe how this definition might be confusing when compared to a finitely generated 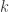 -module. But applying a broader notion of ‘finitely generated’ to both algebras and modules clears up the issue. You can check that the following definition is equivalent to those we’ve seen for algebras and modules. A finitely generated algebra is richer than a finitely generated module because an algebra has an extra operation – multiplication.
-module. But applying a broader notion of ‘finitely generated’ to both algebras and modules clears up the issue. You can check that the following definition is equivalent to those we’ve seen for algebras and modules. A finitely generated algebra is richer than a finitely generated module because an algebra has an extra operation – multiplication.
Definition 4.6 We say an algebra (module) 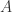 is finitely generated if there exists a finite set of generators
is finitely generated if there exists a finite set of generators 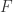 s.t.
s.t. 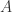 is the smallest algebra (module) containing
is the smallest algebra (module) containing 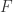 . We then say that
. We then say that 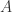 is generated by
is generated by 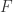 .
.
Theorem 4.7 Let 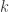 be a general field and
be a general field and 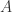 a finitely generated
a finitely generated 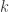 -algebra. If
-algebra. If 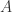 is a field then
is a field then 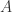 is algebraic over
is algebraic over 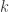 .
.
Okay I cheated a bit saying ‘recall’ Theorem 4.7. You probably haven’t seen it anywhere before. And you might think that it’s a teensy bit abstract! Nevertheless we shall see that it has immediate practical consequences. If you are itching for a proof, don’t worry. We’ll in fact present two. The first will be due to Zariski, and the second an idea of Noether. But before we come to those we must deduce 4.1 – 4.3 from 4.7.
Proof of 4.2 Let ![m \subset k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=m+%5Csubset+k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) be a maximal ideal. Then
be a maximal ideal. Then ![F = k[\mathbb{A}^n]/m](https://s0.wp.com/latex.php?latex=F+%3D+k%5B%5Cmathbb%7BA%7D%5En%5D%2Fm&bg=ffffff&fg=2b2b2b&s=0&c=20201002) a field. Define the natural homomorphism
a field. Define the natural homomorphism ![\pi: k[\mathbb{A}^n] \ni x \mapsto x+m \in F](https://s0.wp.com/latex.php?latex=%5Cpi%3A+k%5B%5Cmathbb%7BA%7D%5En%5D+%5Cni+x+%5Cmapsto+x%2Bm+%5Cin+F&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Note
. Note 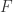 is a finitely generated
is a finitely generated 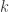 -algebra, generated by the
-algebra, generated by the  certainly. Thus by 4.7
certainly. Thus by 4.7  is an algebraic extension. But
is an algebraic extension. But 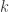 was algebraically closed. Hence
was algebraically closed. Hence 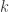 is isomorphic to
is isomorphic to 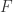 via
via ![\phi : k \rightarrowtail k[\mathbb{A}^n] \xrightarrow{\pi} F](https://s0.wp.com/latex.php?latex=%5Cphi+%3A+k+%5Crightarrowtail+k%5B%5Cmathbb%7BA%7D%5En%5D+%5Cxrightarrow%7B%5Cpi%7D+F&bg=ffffff&fg=2b2b2b&s=0&c=20201002) .
.
Let  . Then
. Then  so
so  . Hence
. Hence  . But
. But 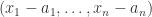 is itself maximal by 3.10. Hence
is itself maximal by 3.10. Hence  as required.
as required. 
That was really quite easy! We just worked through the definitions, making good use of our stipulation that 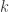 is algebraically closed. We’ll soon see that all the algebraic content is squeezed into the proof of 4.7
is algebraically closed. We’ll soon see that all the algebraic content is squeezed into the proof of 4.7
Proof of 4.1 Let  be a proper ideal in the polynomial ring. Since
be a proper ideal in the polynomial ring. Since ![k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) Noetherian
Noetherian  some maximal ideal. From 4.2 we know that
some maximal ideal. From 4.2 we know that  some point
some point  . Recall from 2.5 that
. Recall from 2.5 that  so
so 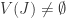 .
. 
The following proof is lengthier but still not difficult. Our argument uses a method known as the Rabinowitsch trick.
Proof of 4.3 Let ![J\triangleleft k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=J%5Ctriangleleft+k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) and
and  . We want to prove that
. We want to prove that  s.t.
s.t.  . We start by introducing a new variable
. We start by introducing a new variable 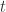 . Define an ideal
. Define an ideal 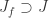 by
by ![J_f = (J, ft - 1) \subset k[x_1,\dots,x_n,t]](https://s0.wp.com/latex.php?latex=J_f+%3D+%28J%2C+ft+-+1%29+%5Csubset+k%5Bx_1%2C%5Cdots%2Cx_n%2Ct%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . By definition
. By definition 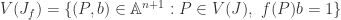 . Note that
. Note that 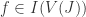 so
so  .
.
Now by 4.1 we must have that 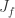 improper. In other words
improper. In other words ![J_f = k[x_1,\dots, x_n, t]](https://s0.wp.com/latex.php?latex=J_f+%3D+k%5Bx_1%2C%5Cdots%2C+x_n%2C+t%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . In particular
. In particular  . Since
. Since ![k[x_1,\dots, x_n, t]](https://s0.wp.com/latex.php?latex=k%5Bx_1%2C%5Cdots%2C+x_n%2C+t%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is Noetherian we know that
is Noetherian we know that  finitely generated by some
finitely generated by some  say. Thus we can write
say. Thus we can write  where
where ![g_i\in k[x_1,\dots , x_n, t]](https://s0.wp.com/latex.php?latex=g_i%5Cin+k%5Bx_1%2C%5Cdots+%2C+x_n%2C+t%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) (*).
(*).
Let 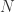 be such that
be such that  is the highest power of
is the highest power of 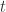 appearing among the
appearing among the  for
for 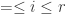 . Now multiplying (*) above by
. Now multiplying (*) above by 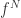 yields
yields  where we define
where we define 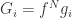 . This equation is valid in
. This equation is valid in ![k[x_1,\dots,x_n, t]](https://s0.wp.com/latex.php?latex=k%5Bx_1%2C%5Cdots%2Cx_n%2C+t%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Consider its reduction in the ring
. Consider its reduction in the ring ![k[x_1,\dots,x_n,t]/(ft - 1)](https://s0.wp.com/latex.php?latex=k%5Bx_1%2C%5Cdots%2Cx_n%2Ct%5D%2F%28ft+-+1%29&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . We have the congruence
. We have the congruence 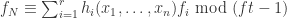 where
where 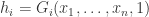 .
.
Now consider the map ![\phi:k[x_1,\dots, x_n]\rightarrowtail k[x_n,\dots, x_n,t]\xrightarrow{\pi} k[x_n,\dots, x_n,t]/(ft-1)](https://s0.wp.com/latex.php?latex=%5Cphi%3Ak%5Bx_1%2C%5Cdots%2C+x_n%5D%5Crightarrowtail+k%5Bx_n%2C%5Cdots%2C+x_n%2Ct%5D%5Cxrightarrow%7B%5Cpi%7D+k%5Bx_n%2C%5Cdots%2C+x_n%2Ct%5D%2F%28ft-1%29&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Certainly nothing in the image of the injection can possibly be in the ideal
. Certainly nothing in the image of the injection can possibly be in the ideal 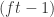 , not having any
, not having any 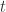 dependence. Hence
dependence. Hence 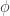 must be injective. But then we see that
must be injective. But then we see that  holds in the ring
holds in the ring ![k[\mathbb{A}^n]](https://s0.wp.com/latex.php?latex=k%5B%5Cmathbb%7BA%7D%5En%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Recalling that the
. Recalling that the  generate
generate  gives the result.
gives the result. 
We shall devote the rest of this post to establishing 4.7. To do so we’ll need a number of lemmas. You might be unable to see the wood for the trees! If so, you can safely skim over much of this. The important exception is Noether normalisation, which we’ll come to later. I’ll link the ideas of our lemmas to geometrical concepts at our next meeting.
Definition 4.8 Let 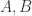 be rings with
be rings with  . Let
. Let  . We say that
. We say that  is integral over
is integral over 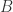 if
if  is the root of some monic polynomial with roots in
is the root of some monic polynomial with roots in 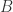 . That is to say
. That is to say 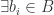 s.t.
s.t. 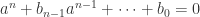 . If every
. If every  is integral over
is integral over 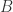 we say that
we say that 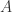 is integral over
is integral over 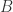 or
or 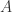 is an integral extension of
is an integral extension of 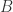 .
.
Let’s note some obvious facts. Firstly we can immediately talk about 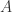 being integral over
being integral over 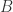 when
when 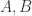 are algebras with
are algebras with 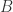 a subalgebra of
a subalgebra of 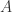 . Remember an algebra is still a ring! It’s rather pedantic to stress this now, but hopefully it’ll prevent confusion if I mix my termin0logy later. Secondly observe that when
. Remember an algebra is still a ring! It’s rather pedantic to stress this now, but hopefully it’ll prevent confusion if I mix my termin0logy later. Secondly observe that when 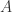 and
and 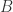 are fields “integral over” means exactly the same as “algebraic over”.
are fields “integral over” means exactly the same as “algebraic over”.
We’ll begin by proving some results that will be of use in both our approaches. We’ll see that there’s a subtle interplay between finite 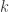 -algebras, integral extensions and fields.
-algebras, integral extensions and fields.
Lemma 4.9 Let 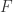 be a field and
be a field and 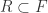 a subring. Suppose
a subring. Suppose 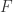 is an integral extension of
is an integral extension of 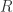 . Then
. Then 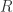 is itself a field.
is itself a field.
Proof Let 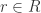 . Then certainly
. Then certainly  so
so 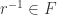 since
since 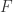 a field. Now
a field. Now 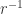 integral over
integral over 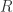 so satisfies an equation
so satisfies an equation 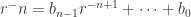 with
with . But now multiplying through by
. But now multiplying through by 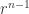 yields
yields  .
. 
Note that this isn’t obvious a priori. The property that an extension is integral contains sufficient information to percolate the property of inverses down to the base ring.
Lemma 4.10 If 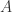 is a finite
is a finite 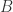 algebra then
algebra then 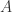 is integral over
is integral over 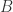 .
.
Proof Write 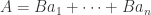 . Let
. Let  . We want to prove that
. We want to prove that  satisfies some equation
satisfies some equation 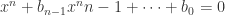 . We’ll do so by appealing to our knowledge about determinants. For each
. We’ll do so by appealing to our knowledge about determinants. For each  we may clearly write
we may clearly write 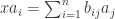 for some
for some 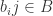 .
.
Writing 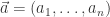 and defining the matrix
and defining the matrix  we can express our equation as
we can express our equation as 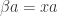 . We recognise this as an eigenvalue problem. In particular
. We recognise this as an eigenvalue problem. In particular  satisfies the characteristic polynomial of
satisfies the characteristic polynomial of 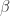 , a polynomial of degree
, a polynomial of degree  with coefficients in
with coefficients in 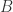 . But this is precisely what we wanted to show.
. But this is precisely what we wanted to show. 
Corollary 4.11 Let 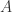 be a field and
be a field and  a subring. If
a subring. If 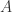 is a finite
is a finite 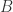 -algebra then
-algebra then 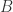 is itself a field.
is itself a field.
Proof Immediate from 4.9 and 4.10. 
We now focus our attention on Zariski’s proof of the Nullstellensatz. I take as a source Daniel Grayson’s excellent exposition.
Lemma 4.12 Let 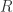 be a ring an
be a ring an 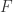 a
a 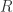 -algebra generated by
-algebra generated by 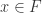 . Suppose further that
. Suppose further that 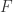 a field. Then
a field. Then  s.t.
s.t. ![S = R[s^{-1}]](https://s0.wp.com/latex.php?latex=S+%3D+R%5Bs%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) a field. Moreover
a field. Moreover  is algebraic over
is algebraic over 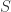 .
.
Proof Let 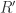 be the fraction field of
be the fraction field of 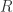 . Now recall that
. Now recall that  is algebraic over
is algebraic over 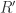 iff
iff ![R'[x] \supset R'(x)](https://s0.wp.com/latex.php?latex=R%27%5Bx%5D+%5Csupset+R%27%28x%29&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Thus
. Thus  is algebraic over
is algebraic over 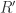 iff
iff ![R'[x]](https://s0.wp.com/latex.php?latex=R%27%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is a field. So certainly our
is a field. So certainly our  is algebraic over
is algebraic over 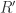 for we are given that
for we are given that 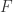 a field. Let
a field. Let  be the minimal polynomial of
be the minimal polynomial of  .
.
Now define 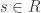 to be the common denominator of the
to be the common denominator of the  , so that
, so that ![f_0,\dots, f_{n-1} \in R[s^{-1}] = S](https://s0.wp.com/latex.php?latex=f_0%2C%5Cdots%2C+f_%7Bn-1%7D+%5Cin+R%5Bs%5E%7B-1%7D%5D+%3D+S&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Now
. Now  is integral over
is integral over 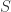 so
so 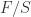 an integral extension. But then by 4.9
an integral extension. But then by 4.9 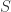 a field, and
a field, and  algebraic over it.
algebraic over it. 
Observe that this result is extremely close to 4.7. Indeed if we take 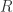 to be a field we have
to be a field we have  in 4.12. Then lemma then says that
in 4.12. Then lemma then says that ![R[x]](https://s0.wp.com/latex.php?latex=R%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is algebraic as a field extension of
is algebraic as a field extension of 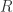 . Morally this proof mostly just used definitions. The only nontrivial fact was the relationship between
. Morally this proof mostly just used definitions. The only nontrivial fact was the relationship between 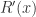 and
and ![R'[x]](https://s0.wp.com/latex.php?latex=R%27%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Even this is not hard to show rigorously from first principles, and I leave it as an exercise for the reader.
. Even this is not hard to show rigorously from first principles, and I leave it as an exercise for the reader.
We’ll now attempt to generalise 4.12 to ![R[x_1,\dots,x_n]](https://s0.wp.com/latex.php?latex=R%5Bx_1%2C%5Cdots%2Cx_n%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . The argument is essentially inductive, though quite laborious. 4.7 will be immediate once we have succeeded.
. The argument is essentially inductive, though quite laborious. 4.7 will be immediate once we have succeeded.
Lemma 4.13 Let ![R = F[x]](https://s0.wp.com/latex.php?latex=R+%3D+F%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) be a polynomial ring over a field
be a polynomial ring over a field 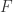 . Let
. Let 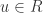 . Then
. Then ![R[u^{-1}]](https://s0.wp.com/latex.php?latex=R%5Bu%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is not a field.
is not a field.
Proof By Euclid, 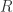 has infinitely many prime elements. Let
has infinitely many prime elements. Let 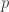 be a prime not dividing
be a prime not dividing  . Suppose
. Suppose ![\exists q \in R[u^{-1}]](https://s0.wp.com/latex.php?latex=%5Cexists+q+%5Cin+R%5Bu%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) s.t.
s.t. 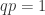 . Then
. Then  where
where 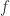 a polynomial of degree
a polynomial of degree  with coefficients in
with coefficients in 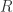 . Hence in particular
. Hence in particular 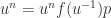 holds in
holds in 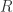 for
for 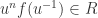 . Thus
. Thus 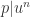 but
but 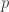 prime so
prime so  . This is a contradiction.
. This is a contradiction. 
Corollary 4.14 Let 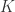 be a field,
be a field, 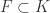 a subfield, and
a subfield, and 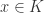 . Let
. Let ![R = F[x]](https://s0.wp.com/latex.php?latex=R+%3D+F%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Suppose
. Suppose  s.t.
s.t. ![R[u^{-1}] = K](https://s0.wp.com/latex.php?latex=R%5Bu%5E%7B-1%7D%5D+%3D+K&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Then
. Then  is algebraic over
is algebraic over 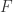 . Moreover
. Moreover  .
.
Proof Suppose  were transcendental over
were transcendental over 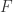 . Then
. Then ![R=F[x]](https://s0.wp.com/latex.php?latex=R%3DF%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) would be a polynomial ring, so by 4.12
would be a polynomial ring, so by 4.12 ![R[u^{-1}]](https://s0.wp.com/latex.php?latex=R%5Bu%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) couldn’t be a field. Hence
couldn’t be a field. Hence  is algebraic over
is algebraic over 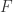 so
so 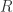 is a field. Hence
is a field. Hence ![R=R[u{-1}]=K](https://s0.wp.com/latex.php?latex=R%3DR%5Bu%7B-1%7D%5D%3DK&bg=ffffff&fg=2b2b2b&s=0&c=20201002) .
. 
The following fairly abstract theorem is the key to unlocking the Nullstellensatz. It’s essentially a slight extension of 4.14, applying 4.12 in the process. I’d recommend skipping the proof first time, focussing instead on how it’s useful for the induction of 4.16.
Theorem 4.15 Take 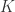 a field,
a field,  a subring,
a subring, 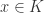 . Let
. Let ![R = F[x]](https://s0.wp.com/latex.php?latex=R+%3D+F%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Suppose
. Suppose  s.t.
s.t. ![R[u^{-1}] = K](https://s0.wp.com/latex.php?latex=R%5Bu%5E%7B-1%7D%5D+%3D+K&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Then
. Then ![\exists 0\neq s \in F s.t. F[s^{-1}]](https://s0.wp.com/latex.php?latex=%5Cexists+0%5Cneq+s+%5Cin+F+s.t.+F%5Bs%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is a field. Moreover
is a field. Moreover ![F[s^{-1}][x] = K](https://s0.wp.com/latex.php?latex=F%5Bs%5E%7B-1%7D%5D%5Bx%5D+%3D+K&bg=ffffff&fg=2b2b2b&s=0&c=20201002) and
and  is algebraic over
is algebraic over ![F[s^{-1}]](https://s0.wp.com/latex.php?latex=F%5Bs%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) .
.
Proof Let  . Now by 4.14 we can immediately say that
. Now by 4.14 we can immediately say that ![L[x]=K](https://s0.wp.com/latex.php?latex=L%5Bx%5D%3DK&bg=ffffff&fg=2b2b2b&s=0&c=20201002) , with
, with  algebraic over
algebraic over  . Now we seek our element
. Now we seek our element  with the desired properties. Looking back at 4.12, we might expect it to be useful. But to use 4.12 for our purposes we’ll need to apply it to some
with the desired properties. Looking back at 4.12, we might expect it to be useful. But to use 4.12 for our purposes we’ll need to apply it to some ![F' = F[t^{-1}]](https://s0.wp.com/latex.php?latex=F%27+%3D+F%5Bt%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) with
with ![F'[x] = K](https://s0.wp.com/latex.php?latex=F%27%5Bx%5D+%3D+K&bg=ffffff&fg=2b2b2b&s=0&c=20201002) , where
, where  .
.
Suppose we’ve found such a 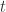 . Then 4.12 gives us
. Then 4.12 gives us 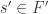 s.t.
s.t. ![F'[s'^{-1}]](https://s0.wp.com/latex.php?latex=F%27%5Bs%27%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) a field with
a field with  algebraic over it. But now
algebraic over it. But now 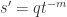 some
some  . Now
. Now ![F'[s'^{-1}]=F[t^{-1}][s'^{-1}]=F[(qt)^{-1}]](https://s0.wp.com/latex.php?latex=F%27%5Bs%27%5E%7B-1%7D%5D%3DF%5Bt%5E%7B-1%7D%5D%5Bs%27%5E%7B-1%7D%5D%3DF%5B%28qt%29%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) , so setting
, so setting 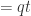 completes the proof. (You might want to think about that last equality for a second. It’s perhaps not immediately obvious).
completes the proof. (You might want to think about that last equality for a second. It’s perhaps not immediately obvious).
So all we need to do is find 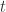 . We do this using our first observation in the proof. Observe that
. We do this using our first observation in the proof. Observe that ![u^{-1}\in K=L[x]](https://s0.wp.com/latex.php?latex=u%5E%7B-1%7D%5Cin+K%3DL%5Bx%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) so we can write
so we can write 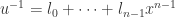 ,
, 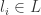 . Now let
. Now let  be a common denominator for all the
be a common denominator for all the  . Then
. Then ![u^{-1} \in F'=F[t^{-1}]](https://s0.wp.com/latex.php?latex=u%5E%7B-1%7D+%5Cin+F%27%3DF%5Bt%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) so
so ![F'[x]=K](https://s0.wp.com/latex.php?latex=F%27%5Bx%5D%3DK&bg=ffffff&fg=2b2b2b&s=0&c=20201002) as required.
as required. 
Corollary 4.16 Let 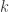 a ring,
a ring, 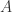 a field, finitely generated as a
a field, finitely generated as a 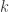 -algebra by
-algebra by  . Then
. Then  s.t.
s.t. ![k[s^{-1}]](https://s0.wp.com/latex.php?latex=k%5Bs%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) a field, with
a field, with 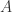 a finite algebraic extension of
a finite algebraic extension of ![k[s^{-1}]](https://s0.wp.com/latex.php?latex=k%5Bs%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) . Trivially if
. Trivially if 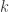 a field, then
a field, then 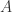 is algebraic over
is algebraic over 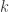 , establishing 4.7.
, establishing 4.7.
Proof Apply Lemma 4.15 with ![F=k[x_1,\dots,x_{n-1}]](https://s0.wp.com/latex.php?latex=F%3Dk%5Bx_1%2C%5Cdots%2Cx_%7Bn-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) ,
, 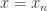 ,
, 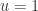 to get
to get 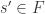 s.t.
s.t. ![A' = k[x_1,\dots,x_{n-1}][s'^{-1}]](https://s0.wp.com/latex.php?latex=A%27+%3D+k%5Bx_1%2C%5Cdots%2Cx_%7Bn-1%7D%5D%5Bs%27%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is a field with
is a field with 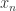 algebraic over it. But now apply 4.15 again with
algebraic over it. But now apply 4.15 again with ![F=k[x_1,\dots,x_{n-2}]](https://s0.wp.com/latex.php?latex=F%3Dk%5Bx_1%2C%5Cdots%2Cx_%7Bn-2%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) ,
, 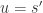 to deduce that
to deduce that ![A''=k[x_1,\dots, x_{n-2}][s''^{-1}]](https://s0.wp.com/latex.php?latex=A%27%27%3Dk%5Bx_1%2C%5Cdots%2C+x_%7Bn-2%7D%5D%5Bs%27%27%5E%7B-1%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is a field, with
is a field, with  algebraic over
algebraic over 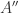 , for some
, for some 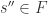 . Applying the lemma a further
. Applying the lemma a further  times gives the result.
times gives the result. 
This proof of the Nullstellensatz is pleasingly direct and algebraic. However it has taken us a long way away from the geometric content of the subject. Moreover 4.13-4.15 are pretty arcane in the current setting. (I’m not sure whether they become more meaningful with a better knowledge of the subject. Do comment if you happen to know)!
Our second proof sticks closer to the geometric roots. We’ll introduce an important idea called Noether Normalisation along the way. For that you’ll have to come back next time!
. That’s because the DBI action which encodes the dynamics of D-branes couples to the dilaton field via a term
. Now recall that the dilaton VEV yields the string coupling and Bob’s your uncle!
? For this, we must remember that D-brane dynamics may equivalently be viewed from an open string viewpoint. To get a feel for the DBI action, we can look at the low energy effective action of open strings. Lo and behold we find our promised factor of
.
. From our new perspective, D-branes aren’t non-perturbative any more!
are worldsheet coordinates,
is the worldsheet metric, and
is the pull-back of the spacetime metric. Clearly conformal invariance is violated unless
.
SYM in 4D from the low energy action of a stack of D-branes. This dimensional conspiracy is lucidly unravelled on page 192 of David Tong’s notes. But even for a 3-brane, the higher derivative operators in the
expansion ruin conformal invariance.




